|
Следующий шаг состоит в вычислении главного собственного вектора. В математических терминах это - вычисление главного собственного вектора, который после нормализации становится вектором приоритетов. В отсутствии ЭВМ, позволяющей точно решить эту задачу, можно получить грубые оценки этого вектора следующими четырьмя способами, которые представлены ниже в порядки увеличения точности оценок.
) Суммировать элемент каждой строки и нормализовать делением каждой суммы на сумму всех элементов; сумма полученных результатов будет равна единице. Первый элемент результирующего вектора будет приоритетом первого объекта, второй - второго объекта, и.т.д.
) Суммировать элементы каждого столбца и получить обратные величины этих сумм. Нормализовать их так, чтобы их сумма равнялась единице, разделить каждую обратную величину на сумму всех обратных величин.
) Разделить элементы каждого столбца на сумму элементов этого столбца (т.е. нормализовать столбец), затем сложить элементы каждой полученной строки и разделить эту сумму на число элементов строки. Это - процесс усреднения по нормализованным столбцам.
) Наиболее точный результат наблюдается при расчете следующим методом, алгоритм, которого, мы рассмотрим более подробно.
-осуществляется перемножение всех элементов каждой строки обратносимметричной матрицы парных сравнений:
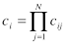 (1) (1)
извлекается корень n-й степени каждого из таких произведений. Получаем главный собственный вектор обратносимметричной матрицы парных сравнений.
-осуществляется нормализация полученных чисел путем разделения элементов каждого столбца на сумму элементов этого столбца.
полученный нормализованный вектор и есть вектор приоритетов.
По известному главному собственному вектору матрицы парных сравнений легко определяется главное собственное число. При этом исходным является уравнение:
 , (2) , (2)
В теории матриц формула (2) отражает тот факт, что w является собственным вектором матрицы С с собственным значением N.
Последовательность расчетов в этом случае сводится к следующей простой схеме.
) Определяется вектор-столбец левой части (2) путем умножения матрицы С на вектор приоритетов 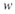 получаем вектор-столбец получаем вектор-столбец 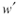
) Вектор-столбец 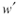 делится покомпонентно на вектор делится покомпонентно на вектор 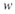 , получается новый вектор , получается новый вектор 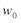 . .
) Вычисляется среднее значение по компонентам 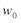 . Эта величина принимается в качестве главного или максимального собственного числа. Таким образом, имеем: . Эта величина принимается в качестве главного или максимального собственного числа. Таким образом, имеем:
)
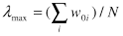 (3) (3)
Заметим, что необходимость перехода к средним вызвана тем, что в соответствии с приведенным выше алгоритмом значения главного собственного вектора вычисляются приближенно. В свою очередь автором, интересующего нас метода анализа иерархий доказано, что собственный вектор обратносимметричной матрицы парных сравнений с наибольшим собственным значением определяет относительное влияние (приоритетность) элементов некоторого уровня на элемент более высокого уровня.
|